P = log10( (1 + Č) ÷ Č) je dle Benfordova zákona matematické vyjádření pravděpodobnosti P, že číslice Č se bude vyskytovat na prvním místě čísel v souboru (téměř) libovolných dat.
Benfordův zákon poprvé objevil v roce 1881 Simon Newcomb. Později (v roce 1938) jej znovuobjevil Frank Benford, podle kterého se následně i jmenuje.
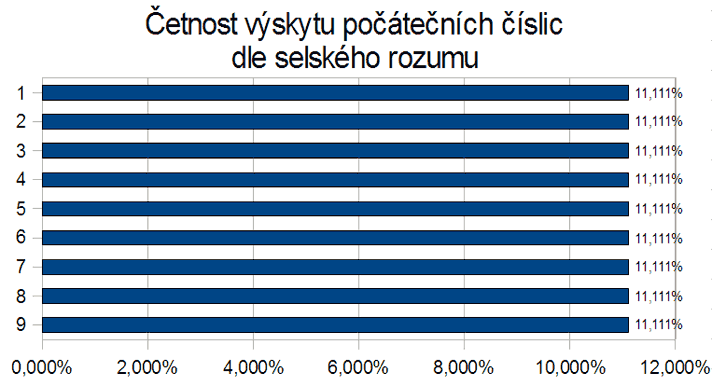
Selský rozum
Tento zákon popisuje jev, který nastává u velkého množství (ne u všech) souborů číselných dat. Selským rozumem by mělo platit, že pravděpodobnost výskytu číslice na prvním místě v souboru dat je stejná pro všechny číslice, tj. 1 ÷ 9 = 11,11% (uvažujeme devět číslic).
Realita
Pozorováním bylo objeveno, že to tak není. Bylo zjištěno, že číslice 1 se na prvním místě vyskutyje v cca 30% případů, číslice 2 v cca 17% a tak dále až k číslici 9, která se na prvním místě vyskutuje v cca 5% případů.
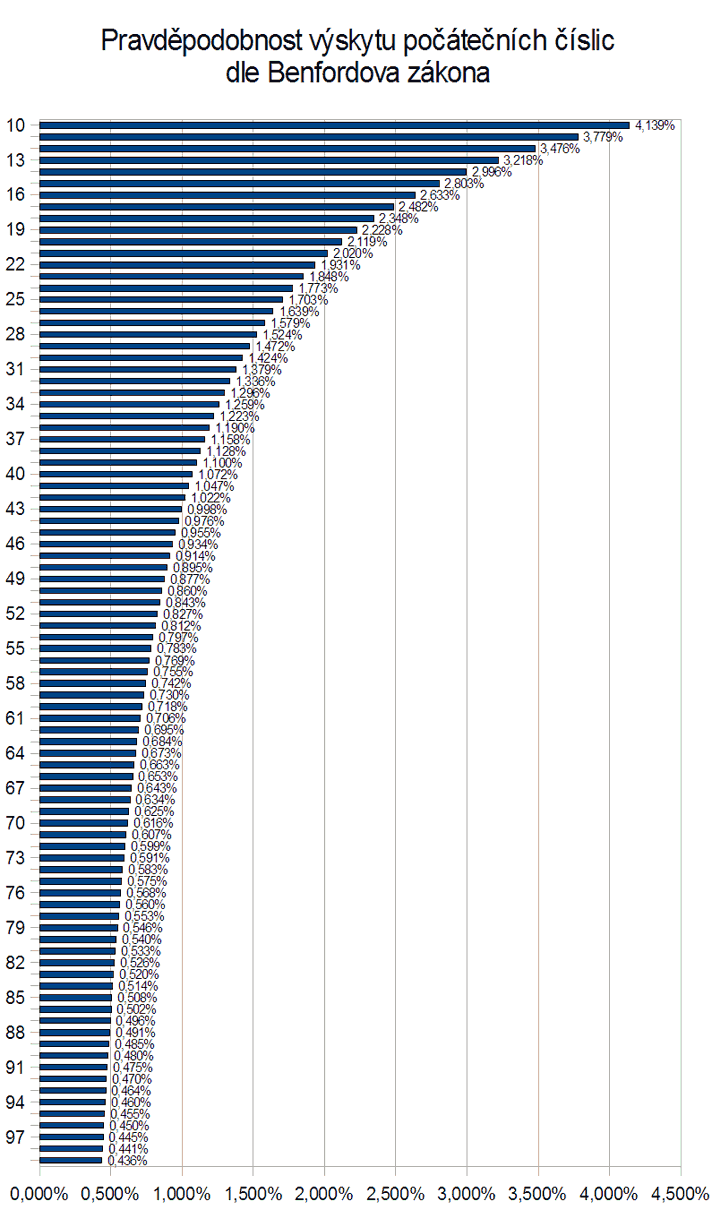
Nejen jedna číslice
Tento zákon lze aplikovat i na více prvních číslic. Pro číslice 1 a 0 platí, že se na prvním místě souboru dat budou vyskytovat s pravděpodobností cca 4%, pro dvě devítky to je již 0,44%.